Calculating battery drain in car audio applications

Duration under Load

Calculating how long a battery will last at a given rate of discharge is not as simple as "amp-hours" - battery capacity decreases as the rate of discharge increases. For this reason, battery manufacturers prefer to rate their batteries at very low rates of discharge, as they last longer and get higher ratings that way. That is fine if you're building a low-power application, but a car audio system really "sucks juice", so you won't be getting the amp-hours you paid for.

The formula for calculating how long a battery will really last has the charming name of "Peukert's Formula". It is...

T = C / Iⁿ

where C is theoretical capacity (in amp-hours, equal to actual capacity at one amp), I is current (in amps), T is time (in hours), and n is the Peukert number for the battery. The Peukert number shows how well the battery holds up under high rates of discharge - most range from 1.1 to 1.3, and the closer to 1, the better. The Peukert number is determined empirically, by testing the battery at different rates. Here is a downloadable XLS file Peukert Calculator.

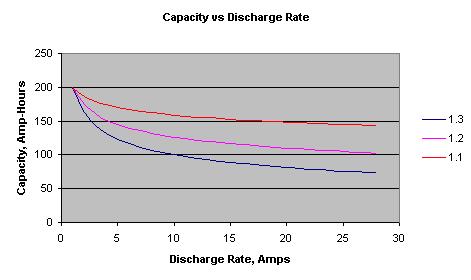
You can see from the graph that a battery with a Peukert's number of 1.3 has half the capacity of a battery with a Peukert's number of 1.1 at a discharge rate of 25 amps, even though they both have the same theoretical capacity (and are probably rated the same by the manufacturers).

Here is a little calculator to play with.

Depth of Discharge and Life Expectancy

Batteries don't last forever - their lifetimes are measured in cycles, or how many times they can be discharged and recharged before they will no longer take a full charge. The depth of discharge (D.O.D.) has a major effect on the life expectancy of a battery - discharging only 80% of the total capacity of the battery will typically get you 25% more cycles than total discharges, and discharging to only 20% will make the battery last essentially forever. Car batteries, however, have to be treated differently - they're not designed to discharge even 20%, and will be damaged if they're deeply discharged. A "deep cycle" battery, on the other hand, can typically survive 400 full discharges.

Multiple Batteries

Very often, one battery won't do the trick - or more likely, you don't have the one that will do the trick, so you're stuck with multiple small batteries.

Hooking batteries in parallel will give you the same voltage as a single battery, but with a Ah and current carrying capacity equal to the sum of the capacities of all the batteries. For example, three 12v 20 Ah batteries in parallel will give you 12v 60 Ah. If each battery could put out 200 amps max, three in parallel could put out 600 amps max.

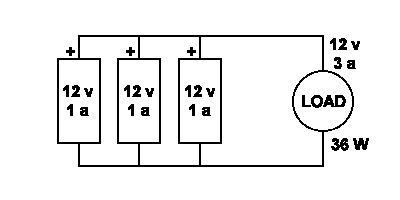
Batteries in Parallel

Hooking the batteries in series will give you a voltage equal to the total voltage of all the batteries, but the Ah and current carrying capacity of only one. For example, three 12v 20 Ah batteries in series will give you 36v 20 Ah. If each battery could put out 200 amps max, then three in series will put out only 200 amps max.

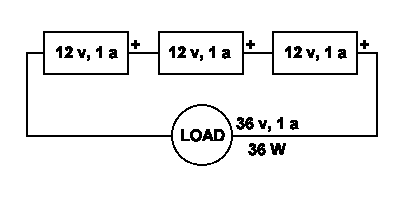
Batteries in Series

In other words, you can combine voltage, or capacity, but not both. In a car you're not really given a choice however, and must wire your batteries in parallel.

Current draw is divided up amongst the batteries the same way that capacity is combined. In parallel, each battery only need supply a fraction of the total current drawn by the load; in series, each battery must supply the full current. Thus, a motor drawing 150 amps from three 12 volt batteries in parallel will draw 50 amps from each.

Power

Electrical power is measured in watts, and is equal to voltage times current:

P = E × I

Notice that while you can combine voltage by putting batteries in series, or combine Ah and current carrying capacity by putting them in parallel, you cannot effect the total power required of the batteries. 12v × 600 A = 36v × 200 A = 72,000 watts either way.

Sample Calculation

Consider an electric car with ten (12 volt, 75 Ah theoretical capacity, 1.1 Peukert) batteries and a 20 hp electric motor that draws 155 amps at 5000 rpm at 120 volts.

As the ten batteries are in series, the current draw is not distributed among the batteries: each battery must provide the full 155 amps to feed the motor. Using the above calculator to figure the capacity of a battery at 155 amps, we get 45.2 Ah. The 100% discharge time will be 45.2 Ah ÷ 155 amps = 0.29 hours, or 17 minutes, so the 80% discharge time will be 14 minutes. If the car is geared to travel at 60 mph at 5000 rpm (and assuming it can reach 60 mph on only 20 hp, which it probably can), it's range will be 14 miles.